Stat 414 – Review 1 Problems

The following are previous exam problems and application problems. The exam this quarter will also involve some more “conceptual” problems as you have been seeing on the quizzes. I also expect interpretation of output I provide. You should assume all of the questions below have “Explain” after them.

1) Knee injuries, like tears in the ACL (a ligament in the knee) can lead to trabecular bone loss and post-traumatic osteoarthritis, but can bone health improve over time? The output below relates to a study on mice where one knee of each of 36 mice had the ACL (a ligament in the knee) ruptured and then measurements were taken of the bone area mass in the knee for both the healthy knees and the injured knees over 56 days after the injury.

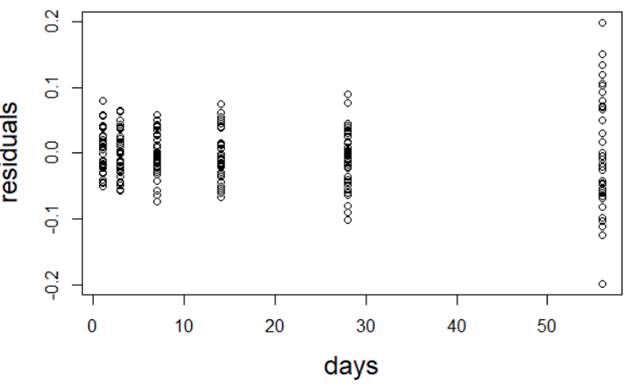
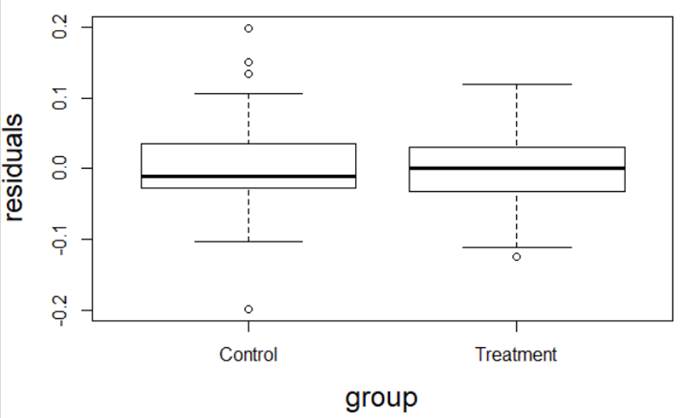
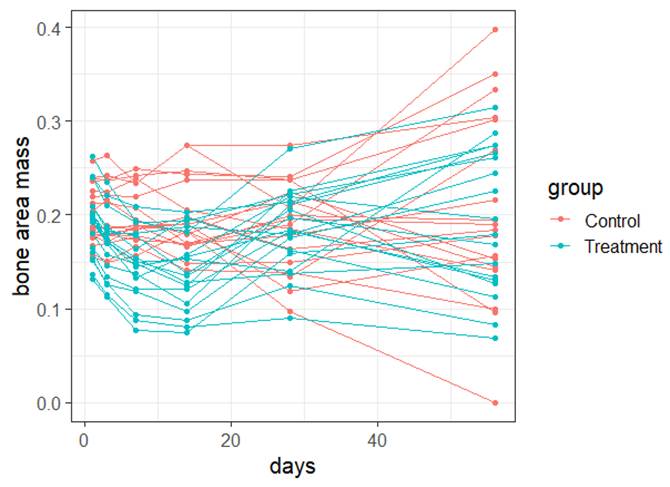
(a) I have fit a rather complicated single-level nonlinear model to these data (using days and group as explanatory variables). Assess the validity of my model. Be very clear how you are evaluating each assumption:

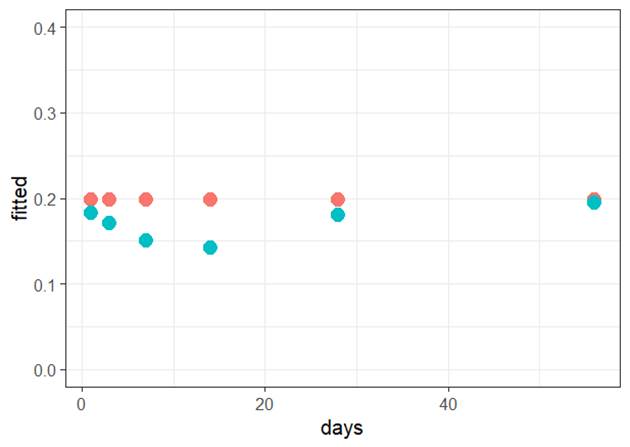
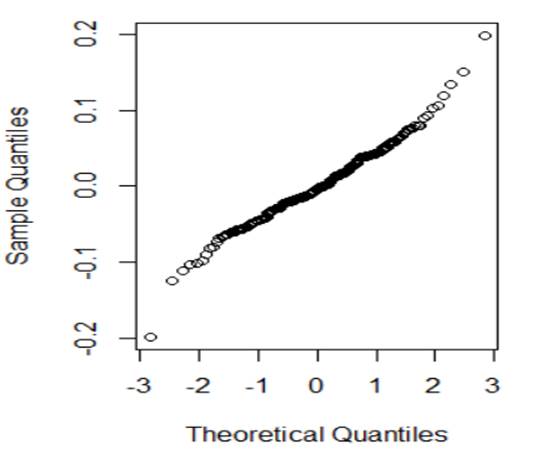
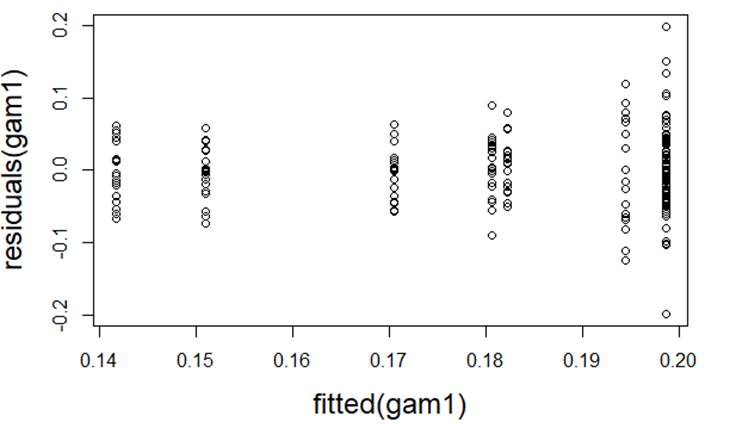
(b) Which of the following would you consider doing next to improve the validity of the model? Briefly justify your choice(s).

· Transformation to improve linearity

· Quadratic model to improve linearity

· Transformation of response to improve normality

· Transformation of explanatory to improve normality

· Include days in a weighted regression

· Include group in a weighted regression

· Multilevel model using mouse as a grouping variable (Level 2 units)

2) Here is another model for the FEV data

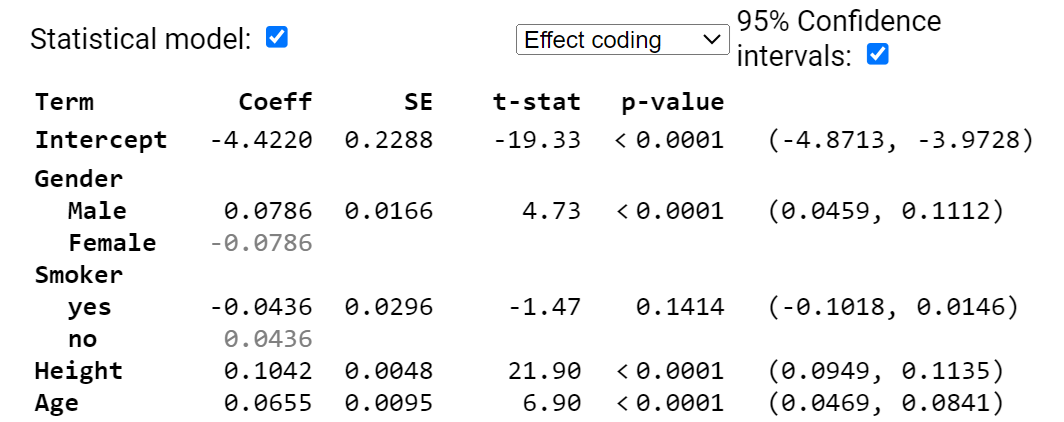
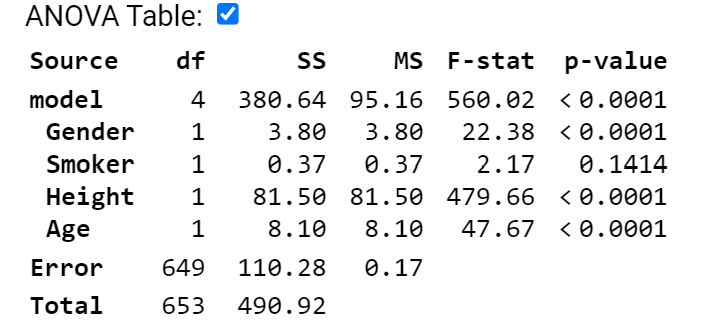
(a) Provide a rough estimate of a 95% confidence interval for a 17-year-old male smoker who is 64 inches tall.

(b) Interpret the (0.0459, 0.1112) interval in context.

(c) Smoker doesn’t appear to be significant in this model. Explain two ways I can tell this?

(d) Can I just remove the smoker variable from the model?

(e) State the null and alternative hypotheses for removing Smoker from the model. Is the p-value for this test in the above output?

(f) If I remove the height variable, smoker is now significant at the 5% level. What does this tell you?

3) Recall our Squid data

Squid$fMONTH = factor(Squid$MONTH)
plot(Testisweight ~ fMONTH, data=Squid)

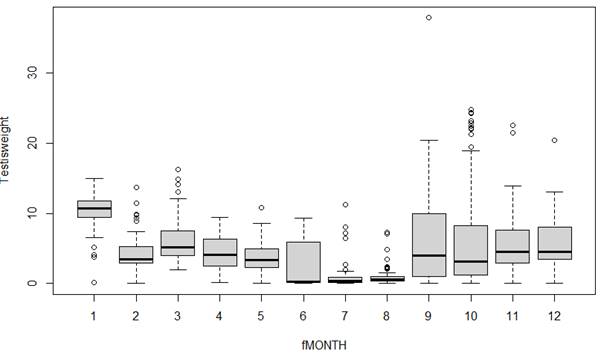
(a) Does there appear to be seasonality in the data? Explain how you are deciding.

(b) Does the variability in the response appear to vary by month? Identify 3 months where you think our predictions of Testisweight will be most accurate. Least?

The graph below shows the predicted values for each month (along with standard errors).

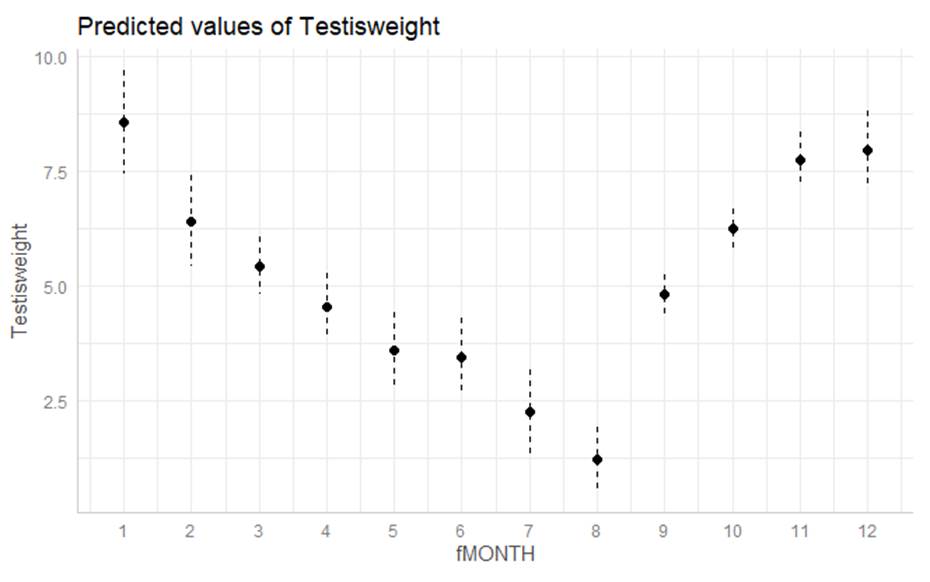
(c) If this model was fit with indicator coding and fMONTH = 1 as the reference group, is the coefficient of fMONTH2 positive or negative?

(d) If this model was fit with effect coding, is the coefficient of fMONTH2 positive or negative?

(e) Continuing (d): If fMONTH1 is the missing category, will its coefficient be positive or negative?

But for addressing the unequal variance: We don't want to assume a "linear relationship" between the variability in the residuals and month number, so we will estimate the variance for each month. We can do that by finding the sample variance for each month.

(f) Which months do we want to 'downweight' in estimating the model?

(g) Conjecture what changes you would expect to see in the previous graph in this weighted regression model.

(h) How do you expect the residual standard error to change in the weighted regression model?

4) Trinh and Ameri (2018) collected data on 1,561 Airbnb listings in Chicago from August 2016, and then they merged in information from the neighborhood (out of 43 neighborhoods in Chicago) where the listing was located. Some of the variables included

· price = price for one night (in dollars)

· overall_satisfaction = rating on a 0-5 scale

· room_type = Entire home/apt, Private room, or Shared room

· TransitScore = quality of the neighborhood for public transit (0-100)

· neighborhood = neighborhood where unit is located (1 of 43)

(a) Identify the Level 1 units and the Level 2 units.

(b) Suppose I want to fit a model that includes the overall satisfaction rating, and transit score. Write the Level 1 and Level 2 equations for a multilevel model.

Consider the following partial output for the multilevel model (Indicator parameterization was used for room size)

Fixed effects:
 Estimate Std. Error t value
(Intercept)  25.353 26.454 0.958
overall_satisfaction 24.919 5.508 4.524
room_typePrivateroom -82.739 3.831 -21.598
room_typeSharedroom -105.875 10.960 -9.660

Number of Observations: 1561

Number of Groups: 43

Analysis of Variance Table

npar Sum Sq Mean Sq F value

room_type 2 2525146 1262573 244.195

overall_satisfaction 1 105350 105350 20.376

(c) Which do you expect to be larger or ? Explain your reasoning.

(d) Interpret the intercept coefficient in context.

(e) Interpret the coefficient of overall_satisfaction in context.

(f) Based on this output, is the type of room statistically significant? State the null and alternative hypothesis in terms of regression parameters, and clearly justify your answer.

(g) Consider the following two variables:

• PctBlack = proportion of black residents in a neighborhood
• HighBlack = 1 if PctBlack above .60, 0 otherwise

Explain why you might choose to use the second variable rather than the first variable in the model. Do you expect the coefficient of HighBlack to be positive or negative? Explain your reasoning.

(h) If HighBlack is added to the model how/if do you expect or to change? Explain your reasoning (for each).

(i) Consider the first few observations of the first row of the 1561 x 1561 variance-covariance matrix for the above model output

Where will the first non-zero value occur?

(j) Here is the first row of the corresponding correlation matrix

Verify the value for 0.0861.

(k) If I were to look at the first row of the corresponding correlation matrix for the null model, how do you think the second value will compare? (likely) Explain your reasoning.

5) Consider the following two models for predicting language scores for 9 different schools. IQ_verb is the student’s performance on a test of verbal IQ.

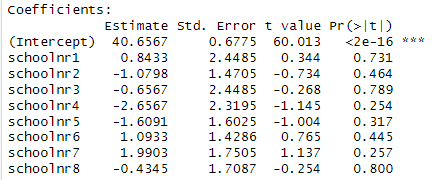
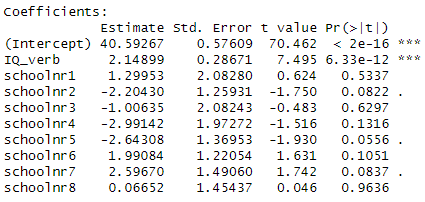
Which model demonstrates more school-to-school variability in language scores?

6) Consider this paragraph: The multilevel models we have considered up to this point control for clustering, and allow us to quantify the extent of dependency and to investigate whether the effects of level 1 variables vary across these clusters.

(a) I have underlined 3 components, explain in detail what each of these components means in the multilevel model.

(b) The multilevel model referenced in the paragraph does not account for “contextual effects.” What is meant by that?

7) Give a short rule in your own words describing when an interpretation of an estimated coefficient should “hold constant” another covariate or “set to 0” that covariate

8) The following SAS output is from modeling results for a randomized controlled trial at 29 clinical centers. The response variable is diastolic blood pressure.

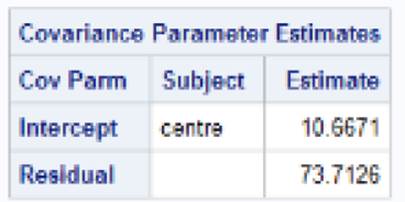
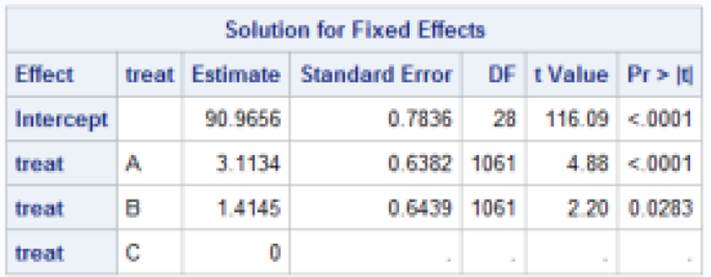
(a) What is the patient level variance? (Clarify any assumptions you are making about the output/any clues you have.)

(b) What is the center level variance?

(c) What is an estimate of the ICC? Calculate and interpret.

(d) What is the expected diastolic blood pressure for a randomly selected patient receiving treatment C at a center with average aggregate blood pressure scores?

(e) What is the expected diastolic blood pressure for a randomly selected patient receiving treatment A at a center with aggregated blood pressure scores at the median?

(f) What is the expected diastolic blood pressure for a randomly selected patient receiving treatment C at a center with aggregate blood pressure scores at the 16th percentile?

(g) What is the expected diastolic blood pressure for a randomly selected patient receiving treatment B at a center with aggregate blood pressure scores at the 97.5th percentile?

9) For a sample of 400 children from the National Longitudinal Survey of Youth, we have data on the child’s cognitive test score at age 3 (“ppvt”), the mother’s level of education, and the mother’s age at the time she gave birth.

Below are the graphs and output related to regressing the ppvt score on the mother’s age

For each assumption below, comment on whether you think it is met. Explain how you are deciding or what additional information you would need. If you think the assumption is violated, explain the nature of the violation.

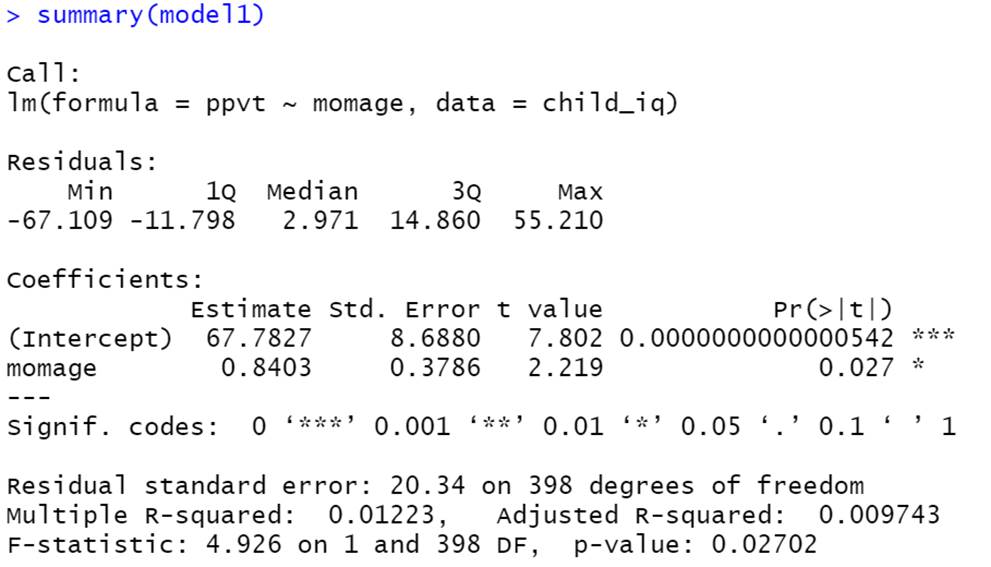
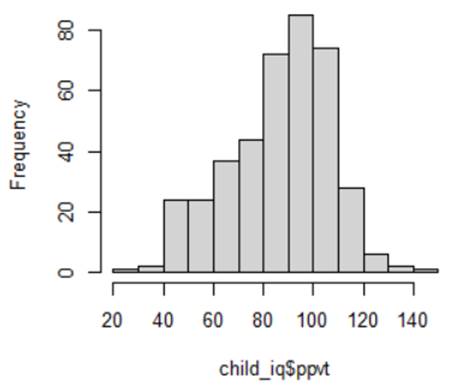
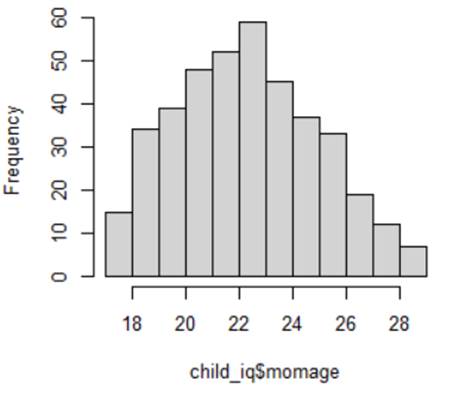
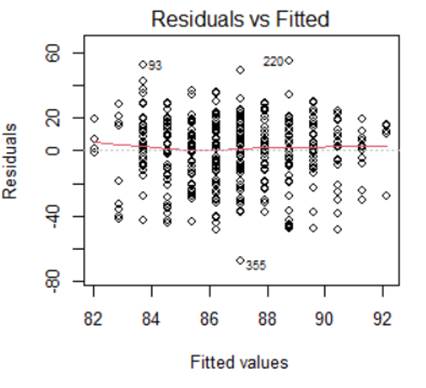
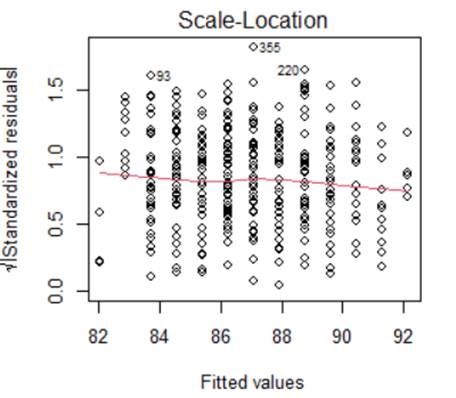
(a) (2 pts) Linearity

(b) (2 pts) Equal variance

(c) (2 pts) Normality

(d) (2 pts) Independence

10) (a) (3 pts) Provide a one-sentence interpretation of the following output

predict(model4, newdata = data.frame(momage=30), interval = "prediction")

fit lwr upr

1 95.89836 56.38459 135.4121

(b) (2 pts) Suppose instead we used interval = "confidence"

1. Identify one thing that will not change

2. Identify one thing that will change