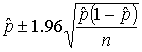 and
and 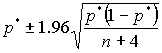 ,
,A Data-Oriented, Active Learning, Post-Calculus Introduction to Statistical Concepts, Methods, and Theory.
Allan Rossman, Beth Chance, Karla Ballman
to be presented at Joint Statistical Meetings, August 2000
Abstract
We describe this NSF-funded project to develop a two-course sequence that introduces post-calculus students to statistical concepts, methods, and theory. These courses provide a more balanced introduction to the discipline of statistics than the standard sequence in probability and mathematical statistics. The materials incorporate many features of successful statistics education projects that target less mathematically prepared students. Such features include developing students' conceptual understanding of fundamental ideas, promoting student explorations through hands-on activities, analyzing genuine data drawn from a variety of fields of application, and integrating computer tools both to enhance students' learning and to analyze data efficiently. Our proposed introductory course differs by utilizing students' calculus knowledge and mathematical abilities to explore some of the mathematical framework underlying statistical concepts and methods. Distinguishing the second course is the use of simulation, computer graphics, and genuine problems and data to motivate and illustrate statistical theory. In this presentation, we outline the goals, content, and pedagogy of this sequence. We also present examples of student activities from both courses.
I. BACKGROUND
The past decade has seen the development of a reform movement in statistics education, emphasizing features such as statistical thinking, active learning, conceptual understanding, genuine data, use of technology, collaborative learning, and communication skills. [See, for example, Cobb (1992), Cobb (1994), and Moore (1997) for overviews of this reform movement.] A wide variety of materials have been developed to support this type of instruction [see Moore (2000) for descriptions of such teaching resources]:
As these materials become more readily available, noticeable changes are occurring in introductory courses, especially in the areas of teaching methods, course content, and use of technology [see, for example, Garfield, in press].
However, the vast majority of these efforts have been directed at what we will call "Stat 101," an introductory, algebra-based, service course for non-majors. Relatively little attention has been paid to introductory statistics courses for mathematically inclined students majoring in fields such as mathematics, economics, the sciences, engineering, and even statistics.
II. THE PROBLEM
Mathematics majors and other students with strong mathematical backgrounds typically choose between two options for introductory study in statistics: 1) take the Stat 101 course, or 2) take a standard two-semester sequence in probability and mathematical statistics. The first option is far from ideal, because the Stat 101 course is aimed at a different student audience and is not at a challenging mathematical level. Due to its lack of substantial mathematical content, this course often does not count towards the student's major, providing a strong disincentive from taking the course.
Unfortunately, the second and more common option is also fraught with problems. Concerns about the nature of this sequence are not new. For example, the 1980 report of the MAA's Committee on the Undergraduate Program in Mathematics (CUPM) stated: "The traditional undergraduate course in statistical theory has little contact with statistics as it is practiced and is not a suitable introduction to the subject." This "math stat" sequence often presents a full semester of probability before proceeding to statistics, and then the statistics covered is often abstract in nature. As a result, students do not emerge from the sequence with a modern and balanced view of the applied as well as the theoretical aspects of the discipline of statistics. In fact, students often leave this course with less intuition and conceptual understanding than students who have taken a lower level course (e.g. data collection issues, statistical vs. practical significance, association vs. causation, robustness, diagnostics). An unfortunate consequence of this may be that the courses fail to attract some good students who would be excited by statistical applications.
Furthermore, the "math stat" sequence also does not typically adopt the pedagogical reform features (e.g. active learning, conceptual focus, group work, written reports) that have been demonstrated to enhance student learning (Garfield, 1995). This is particularly problematic when these courses aim to prepare future teachers of statistics. Students emerging from a traditional "math stat" sequence generally do not experience a model of data-oriented, activity-based teaching practices that they will be expected to adopt in keeping with NCTM Standards or as teachers of AP Statistics.
There have been some efforts to incorporate more data and applications into the "math stat" sequence. Moore (1992) provides several examples for how he infuses the second semester course with more data and concrete applications, and Witmer (1992) offers a supplementary book towards these goals. Texts such as Rice (1994) include more genuine data and applied topics such as two-way ANOVA and normal probability plots. More recently, a new text by Terrell (1999) aims to present a "unified introduction" to statistics by using statistical motivations for probability theory; its first two chapters are devoted to structural models for data and to least squares methods, before the introduction of probability models in chapter 3. Additionally, a new supplement by Nolan and Speed (2000) provides lab activities that integrate real scientific applications into statistical investigations in order to motivate the theory presented.
These changes are directed toward the second course in the two-course sequence, presumably leaving the first course to cover probability theory. This approach is especially a disservice to students who only take the first course. These students (e.g. engineering majors, mathematics education majors) often just do not have room in their curriculum for a second course. Other students, failing to see the relevance to their own discipline, may simply choose not to continue to the second course. As a consequence, Berk (1998) advocates that "we should maximize the amount of statistics in the first semester."
Thus, while there have been efforts, they have not yet achieved the widespread integration into the entire sequence as has been hoped. As David Moore wrote in support of our grant proposal in 1998: "The question of what to do about the standard two-course upperclass sequence in probability and statistics for mathematics majors is the most important unresolved issue in undergraduate statistics education." We propose a rethinking of the entire two-course sequence so that the first course also addresses the call of Cobb and Moore (1997) to "design a better one-semester statistics course for mathematics majors."
III. COURSE MATERIALS
In response to this challenge, we are developing curricular materials for a two-course sequence at the post-calculus level, introducing mathematically inclined students to statistical concepts, methods, and theory through a data-oriented, active learning pedagogical approach. We consider it essential that the first course provide a self-contained introduction to statistics, focusing on concepts and methods but also introducing some of their mathematical underpinnings. The materials provide a mixture of activities and exposition, with the activities leading students to explore statistical ideas and construct their own conceptual understanding.
The principles guiding our development of these course materials are:
While several of these principles are equally relevant to the Stat 101 course, the focus on mathematical underpinnings sets this sequence apart. Students also develop several strategies for addressing problems; for example, the use of simulation as an analysis tool and not just as a learning device is emphasized throughout. With regard to use of technology tools, students use spreadsheet programs and computer algebra systems as well as statistical analysis packages., The focus is on a modern approach to these problems. Students will still learn basic rules and properties of probability, but in the context of statistical issues. Students will be motivated by a recent case study or statistical application and when necessary will "detour" to a lesson in the appropriate probabilistic technique. In each scenario, students will follow the problem from the origin of the data to the final conclusion.
The pedagogical approach will be a combination of investigative activities and exposition. Some of the activities will be quite prescriptive, leading students clearly to a specific learning outcome, while others will be very open-ended. Examples of the former include guiding students to discover that the power of a test increases as the sample size does (other factors being equal), while examples of the latter include asking students to suggest and examine the performance of alternatives to the chi-square statistic for assessing goodness-of-fit.
We are planning the sequencing of topics with three objectives in mind. First, generally speaking, we aim to introduce concepts first, followed by methods, and then theory. This certainly does not mean that we will cover all of the concepts and then all of the methods and then all of the theory. Rather, we mean to emphasize that students' first exposure to an idea is on the conceptual level in a genuine context, then they are introduced to methods of application, and finally are students introduced to the theoretical foundation.
The second objective with regard to sequencing is to repeatedly model the process of statistical inquiry from data collection through data analysis and statistical inference. The third is to frequently re-visit important ideas in new settings. To accomplish these goals, we propose to adopt a "change one thing at a time" approach to sequencing. For example, the first chapter presents a randomized comparative experiment with binary variables and small sample sizes, focusing on concepts of experimentation, randomization, comparison, and significance. The next chapter treats the same situation but deals with observational studies, emphasizing that while the mathematics of the analysis remains the same, the scope of one's conclusions changes greatly. The third chapter then moves to the case of a single sample, the fourth to large sample sizes, and the fifth to the goal of estimation as opposed to comparison. The sixth chapter finally re-examines all of these ideas and repeats the analyses for quantitative as opposed to binary variables. [A preliminary outline of topics appears in the Appendix.]
IV. SAMPLE ACTIVITIES
Below we present descriptions of five sample activities in order to provide a better sense for the materials being developed. We have chosen these both to illustrate the course principles described above and also to highlight differences between activities for a Stat 101 course and for the more mathematically inclined audience that we are addressing.
Sample Activity 1 (from chapter 1 of the preliminary outline) presents the first activity in our proposed course, introducing students to fundamental issues of experimentation, randomization and statistical significance. Sample Activity 2 (from chapter 3) follows students' introduction to one-sample tests about a population proportion based on the binomial distribution; it expands students' use of simulation to explore issues of power and type I vs. type II error rates. Sample Activity 3 (from chapter 5) addresses the goal of estimation and specifically the concept of confidence. Properties of measures of center are explored in Sample Activity 4 (from chapter 6). Sample Activity 5 (from chapter 8) presents the idea of maximum likelihood.
This activity concerns a psychology experiment to study whether having an observer with a vested interest in a subject's performance on a cognitive task detracts from that performance (Butler & Baumeister, 1998). Twenty-three subjects played a video game ten times to establish their skill level. They were then told that they would win a prize in the next game if they surpassed a threshold value chosen for each individual so that he/she had beaten it three times in ten practice games. Subjects were randomly assigned to one of two groups. One group (A) was told that their observer would also win a prize if the threshold was surpassed; the other (B) was told nothing about the observer winning a prize. Results of the study are summarized in the table:
|
group A |
group B |
total |
|
|
surpassed threshold |
3 |
8 |
11 |
|
did not beat threshold |
9 |
3 |
12 |
|
total |
12 |
11 |
23 |
Students are asked to use cards (11 black cards for "winners" who surpass the threshold and 12 red cards for "losers") to simulate random assignment of these subjects to treatment groups, under the assumption that group membership has no effect on performance. They pool their results in class to obtain an approximate sampling distribution of the number of "winners" randomly assigned to group A. By determining the proportion of cases in which that number is three or less, they approximate the p-value of the randomization test. Students thus begin to develop an intuitive understanding of the concept of statistical significance and an appreciation that statistical inference asks the fundamental question, "How often would such sample results occur by chance?"
To this point the activity is very similar to ones appropriate for Stat 101 students, for example as found in Activity-Based Statistics (Scheaffer, et. al., 1996) and Workshop Statistics (Rossman and Chance, 2001). With this audience of mathematically inclined students, however, it is appropriate to ask them to take the next step and to calculate the exact p-value using hypergeometric probabilities. Thus, we take this occasion to develop the hypergeometric distribution by studying counting rules and combinations and the equal likeliness assumption, motivated by their preliminary investigations. This probability "detour" comes "just in time" for students to explore with more precision the statistical concept of significance in the context of real data from a scientific study.
We ask students to consider a baseball player who has been a .250 career hitter but genuinely improves to the point of becoming a .333 hitter, a very practically significant difference in this context. The question then is how likely the player is to establish that he has improved in a sample of 30 at-bats. Again we ask students to investigate this issue first through simulation. They use technology to simulate the results of 1000 samples of 30 at-bats for a .250 hitter and also for a .333 hitter, note the substantial overlap between the two distributions, and estimate the (low) power of the test from the simulation results. They then increase the sample size and note the resulting increase in power. At that point we ask students to study the binomial distribution and to apply it, with the benefit of technology, to calculating the exact power of these tests. They then set up their statistical or spreadsheet package to perform these calculations efficiently for a variety of user-supplied sample sizes, significance levels, and values of the alternative probability. Finally, students conclude the activity by sketching graphs of power vs. these factors and writing a report (to either the player or manager) explaining the effects of these factors on power.
We then continue with this context and ask students to calculate a and b, probabilities of type I and type II errors, respectively, for various values of the rejection region X > k. We ask students to graph a vs. b to see the inverse relationship between them. We also ask students to graph a+b and to determine the rejection region that minimizes this sum. Finally, students consider the possibility that the consequences of type I error might be deemed c times more serious than those of type II error and so minimize ca+ b for various values of c.
While a side benefit of these activities is that students become familiar with the binomial distribution and with calculations involving it, the emphasis is on helping them to understand the concepts of power and of type I and type II errors. Technology again serves as an indispensable tool for minimizing computational burdens, enabling students to explore these ideas and develop their own understandings of them.
As with Stat 101 students, students in this course begin to study the concept of confidence as they study sampling distributions through physical and then technology simulations. We then ask these students to use their mathematical abilities to investigate the meaning of "confidence" more formally through a follow-up to the Activity-Based Statistics activity that leads students to view a confidence interval as the set of plausible values of a population parameter based on the observed sample. Students use their knowledge of the binomial distribution along with technology to create exact binomial confidence intervals for a population proportion. They do this by considering all parameter values from .001 to .999 and calculating the probability of obtaining a sample proportion as extreme as the actual with each proposed parameter value. Parameter values for which this probability exceeds a/2 are considered plausible and are therefore included in the 100(1-a)% confidence interval. Through this activity students also discover the duality between confidence intervals and two-sided tests of significance.
We then present students with two formulas for constructing approximate, large-sample 95% confidence intervals for a population proportion:
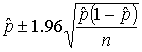 and
and 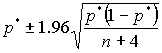 ,
,
where ![]() is the ordinary sample proportion of "successes" and
is the ordinary sample proportion of "successes" and ![]() is an estimator that "shrinks" the sample proportion toward one-half.
is an estimator that "shrinks" the sample proportion toward one-half.
The former, of course, is the standard technique based on the normal approximation to the binomial distribution, and the second was proposed by Agresti and Coull (1998). We ask students to compare the performance of these two interval estimators. This question naturally leads to a discussion of coverage probabilities and of interval lengths, and we proceed to ask students to perform simulations to determine coverage rates of both types of intervals for various values of the sample size n and the parameter value p. Students find that for values of n and p with np < 10, the standard procedure produces nominal 95% confidence intervals that actually contain the population parameter less often than claimed, whereas the second procedure achieves a coverage rate much closer to the nominal confidence level.
These exercises achieve several goals. First, they help students to deepen their understanding of confidence level as a coverage probability under repeated sampling. Second, they afford students the opportunity to investigate and evaluate recently published statistical methods, demonstrating the dynamic nature of the discipline. Finally, they provide students with still more experience of the utility of simulation as a powerful problem-solving tool. Whereas with Stat 101 students we try to make the simulations very easy, even transparent, to run, we expect these students to implement the details of the simulation procedure themselves.
We provide students with data on the total points scored in the ten National Basketball Association games played on December 10, 1999:
140, 163, 184, 190, 196, 198, 204, 205, 206, 224
We ask students to propose criteria for comparing point estimates of the center of this distribution. Common criteria suggested include the sum of absolute deviations between the data values and the estimate, and the sum of squared deviations:
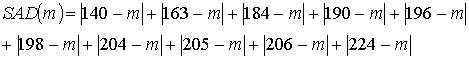
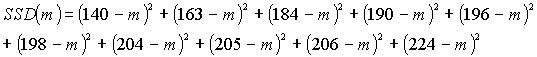
Students investigate the behavior of these functions, analytically and graphically, and discover that the SAD function has an interesting piecewise linear appearance, minimized not at a unique value but for any value between 196 and 198 (the two middle data values), inclusive. Naturally, the SSD function is parabolic, minimized at the sample mean. Students then use their calculus skills to prove that the sum of squared deviations is always minimized at the sample mean. In addition to examining these mathematical properties, students also use this activity to explore properties such as resistance of the median but not the mean to outliers. They also investigate other criteria, finding for example that the midrange minimizes the maximum absolute (or squared) deviation. This activity also provides an introduction to the fundamental notion of "residual."
We ask students to consider estimating how many three-letter words are in the English language. Groups of students use one of three different sampling designs to collect data. One group generates random three-letter strings until the first English word appears, another does so until five English words appear, and a third generates 100 random strings and counts how many words result. Students then use technology to graph the likelihood function of p, the probability that a random three-letter string will form a legitimate English word, for their sampling design and data. They then graph the likelihood function as a function of N, the number of three-letter English words. Identifying the maximum value as a point estimate leads them to discover that the invariance property of MLE's holds in this case. Finally, students use their calculus skills to determine the maximum likelihood estimators for each of the three sampling designs. An extension of this activity asks them to restrict attention to only the ten most common letters and to collect data and perform the analysis again.
This activity introduces students to the idea of a likelihood function and to the use of a method for determining point estimators of parameters. It allows them to collect data in a fun context and gives them more practice working with probability distributions in a statistical setting. Re-emphasizing the importance of sampling design in determining one's analysis, the activity also uses technology to emphasize the graphical, visual elements of that analysis.
V. CONCLUSION
We have argued that while the statistics education reform movement has made great strides and produced important materials for revamping "Stat 101" courses, a pressing need to reform introductory statistics courses for mathematically inclined students persists. We propose to address this need by developing materials to support a data-centered, active learning pedagogical style at the post-calculus level. Some of the key features of these materials are illustrated in common elements of the sample activities presented above, including:
Our hope is that this re-designed course sequence will provide a more balanced introduction to statistical concepts and methods as well as theory, will increase interest in statistics as a potential career or side interest among mathematically inclined students, and will better prepare future teachers to employ student-centered pedagogy in their future classes.
References:
Agresti, A. and Coull, B. (1998), "Approximate is Better than 'Exact' for Interval Estimation of Binomial Proportions," The American Statistician, 52, 119-126.
Berk, K. (1998), "Revamping the Mathematical Statistics Course" in 1998 Proceedings of the Section on Statistical Education, American Statistical Association.
Butler, J. and Baumeister, R. (1998), "The Trouble with Friendly Faces: Skilled Performance with a Supportive Audience," Journal of Personality and Social Psychology, 75, 1213-1230.
Cobb, G. (1992), "Teaching Statistics" from Heeding the Call for Change: Suggestions for Curricular Action, ed. L. Steen, Mathematical Association of America, Notes #22, 3-43.
Cobb, G. (1995), "Reconsidering Statistics Education: A National Science Foundation Conference", Journal of Statistics Education, 1(1).
Cobb, G. and Moore, D. (1997), "Mathematics, Statistics, and Teaching", The American Mathematical Monthly, 104, 801-824.
CUPM (1981), "Recommendations for a General Mathematical Sciences Program," Mathematical Association of America.
Garfield, J. (1995), "How Students Learn Statistics". International Statistical Review. 63(1). 25-34.
Garfield, J. (2000), "An Evaluation of the Impact of Statistics Reform: Year 1 Report," funded by the National Science Foundation, REC-9732404.
Moore, D. (1997). "New Pedagogy and New Content: The Case of Statistics" (with discussion). International Statistical Review. 65, 123-165.
Moore, T. (1992), "Getting More Data into Theoretical Statistics Courses". Primus: Problems, Resources, and Issues in Undergraduate Mathematics Studies, 2, 348-356.
Moore, T., ed. (2000), Teaching Resources for Undergraduate Statistics, Mathematical Association of America, Notes #51.
Nolan, D. and Speed, T. (2000), Stat Labs: Mathematical Statistics Through Applications, Springer-Verlag.
Rice, J. (1994), Mathematical Statistics and Data Analysis, second edition, Wadsworth Publishing Co.
Rossman, A. and Chance, B. (2001), Workshop Statistics: Discovery with Data, second edition, Key College Publishing.
Scheaffer, R., Gnanadesikan, M., Watkins, A., and Witmer, J. (1996), Activity-Based Statistics. Springer-Verlag.
Terrell, G. (1999), Mathematical Statistics: A Unified Introduction, Springer-Verlag.
Witmer, J. (1992), Data Analysis: An Introduction, Prentice-Hall.
A Data-Oriented, Active Learning, Post-Calculus Introduction to Statistical Concepts, Methods, and Theory
Preliminary Content Outline June 2000
Allan Rossman, Beth Chance, Karla Ballman
Some Principles:
Format:
Roughly half activities, half exposition
Sequencing:
Change scenarios "one component at a time"
(The first course would probably end about here.)
Chapter 1: Variation, Randomness, and Comparisons
Introduce idea of statistical significance in a setting of comparing experimental groups
(Scenario: categorical variables, two groups, small samples, experiment, comparison)
Chapter 2: Observation, Confounding, Causation
Compare/contrast conclusions to be drawn from controlled experiments vs. observational studies
(Scenario: categorical variables, two groups, small samples, observational study, comparison)
Chapter 3: Sampling
Introduce idea of random sampling and its associated concepts, binomial model
(Scenario: categorical variables, one group, small samples, comparison)
Chapter 4: Large-Sample Approximations
Study normal approximations to above analyses for large samples
(Scenario: categorical variables, large samples, comparison)
Chapter 5: Estimation
Introduce concept of confidence, interval estimation; apply to situations studied thus far
(Scenario: categorical variables, estimation)
Chapter 6: Quantitative Variables
Repeat all of the above analyses (graphical, numerical, inferential) with quantitative variables
(Scenario: quantitative variables)
Chapter 7: Bivariate Data, Association, Prediction
Investigate concepts related to association and prediction, emphasize model basics (data = fit + residual), apply in specific settings
Chapter 8: Probability Models, Distributions
Study "catalog" of common distributions as models, introduce estimation principles
Chapter 9: Theory of Testing, Decision
Investigate more theoretical aspects of testing and decision theory
Chapter 10: Linear Models
Study common structure, applicability of linear models