Statistical Inference - Central Limit Theorem
Now let's consider instead using the Central Limit Theorem for a Sample Proportion (as opposed to simulation) to approximate this probability. There are "conditions" to when it is ok to do so (Topic 13):
- Randomness: We have a random sample from the population of interest
- Sample size: We have a large enough sample size, where large enough is checked by seeing whether n x
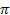is at least 10 and n x (1- 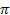) is at least 10.
(i) To check the sample size condition, calculate the 2 products, using the hypothesized value of , and compare each to 10. (Show your work.) Does this condition appear to be met?
(j) What does the Central Limit Theorem for a Sample Proportion (CLT) predict for the shape, mean, and standard deviation of the sampling distribution of the sample proportion (assuming the null hypothesis is true)?
Use this Normal model specified by the CLT, and the Normal Probability Calculator applet (below), to determine the probability of interest:
- Specify an appropriate axis label for the sampling distribution we are considering in the variable box in the Normal Probability Calculator applet below, then plug in the mean and standard deviation values from the CLT(at least 3 decimal places each), and press Scale to Fit.
- Specify the value of our sample proportion in the X box.
- Toggle the < symbol to be > to find the area above our value. Press Enter/Return on your keyboard.
Normal Probability Calculator Applet
Below is an internet applet you are to use for this lab. See these hints if you have trouble using the applet.
Include a screen capture of the applet in your report including the graph and the z-value and probability output.
(k) Provide a detailed interpretation of the z-value in this context.
(l) How does the estimate of the p-value between the two methods (simulation in part g and Central Limit Theorem) compare? Were they similar? Did you expect them to be similar based on your check of the conditions for the Central Limit Theorem? Explain.
(m) Provide a detailed interpretation of this p-value in this context (recall lessons from earlier labs).
(n) Is this p-value small enough to convince you that there is a genuine tendency for students at your school to pick scissors less than 1/3 of the time? Explain your reasoning. (Recall the p-value cut-offs from Lab 1.)
